समकोण त्रिभुज की परिभाषा

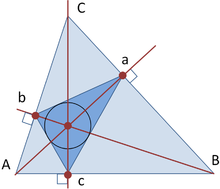
यदि हम आयतों के बारे में बात करते हैं तो हम गणितीय ज्ञान के क्षेत्र में हैं, और विशेष रूप से, ज्यामिति में। समकोण त्रिभुज की एक विशेषता है: यह एक त्रिकोणीय ज्यामितीय आकृति है जिसमें इसकी एक भुजा 90 डिग्री मापी जाती है और इसकी दो शेष भुजाएँ पहले के विपरीत होती हैं और इसे पैर कहा जाता है। सबसे बड़ा पक्ष जो इसे बनाता है उसे कर्ण के रूप में जाना जाता है और यह हमेशा पैरों द्वारा बनाए गए कोण का विरोध करता है।

पाइथागोरस प्रमेय

समकोण त्रिभुज में दो न्यून कोण और एक समकोण होता है। कोणों की इस संरचना से इन त्रिभुजों के त्रिकोणमितीय अनुपातों की गणना करना संभव है। इस तरह, यदि एक समकोण त्रिभुज में सबसे लंबी भुजाएँ 13 सेमी और 12 सेमी मापती हैं, तो पाइथागोरस प्रमेय को लागू करके सबसे छोटे न्यून कोण की दूरी की गणना करना संभव है (इस मामले में अंतिम परिणाम 25 से कम कोण होगा डिग्री, चूंकि पाइथागोरस प्रमेय कहता है कि एक समकोण त्रिभुज में कर्ण का वर्ग पैरों के वर्गों के योग के बराबर होता है)।

व्यावहारिक अनुप्रयोग और समकोण त्रिभुजों की उपस्थिति

पाइथागोरस का जन्म ग्रीक द्वीप समोस में ईसा पूर्व Vl सदी में हुआ था। सी। उनका प्रमेय सभी प्रकार के विषयों में वास्तविक समस्याओं की गणना और हल करने के लिए एक मौलिक उपकरण है: वास्तुकला, कार्टोग्राफी, भूगोल, शहरी नियोजन, आदि। ये और अन्य सैद्धांतिक विषय व्यावहारिक प्रश्नों को हल करने की अनुमति देते हैं, क्योंकि एक समकोण त्रिभुज का आकार शहर के नक्शे पर, दीवार के खिलाफ झुकी हुई सीढ़ी पर, या खेल के मैदान के कोणों पर पाया जा सकता है।

समकोण त्रिभुज की अवधारणा रोजमर्रा की जिंदगी में एक वास्तविकता बन जाती है और वास्तव में, यह सभी प्रकार की परिस्थितियों और स्थितियों (एक घर की छत, एक ज्यामितीय आकार के मूर्तिकार या नाव की पाल में) में प्रकट होती है।

अन्य त्रिभुज

सभी त्रिभुजों में आवश्यक रूप से खण्डों से जुड़े हुए 3 बिंदु होते हैं। यदि हम त्रिभुजों को उनकी भुजाओं के अनुसार वर्गीकृत करते हैं, तो हमारे पास एक समबाहु त्रिभुज होता है जिसकी तीन बराबर भुजाएँ होती हैं, समद्विबाहु की दो समान भुजाएँ होती हैं और स्केलीन की कोई भी भुजा समान नहीं होती है। त्रिभुजों को वर्गीकृत करने का दूसरा तरीका उनके कोणों को ध्यान में रखना है। इस वर्गीकरण के अनुसार, उपरोक्त समकोण त्रिभुज (याद रखें कि इसमें 90 डिग्री का कोण है) के अलावा, न्यूनकोण त्रिभुज (तीन कोण 90 डिग्री से कम हैं) और अधिक त्रिभुज (कोणों में से एक है) भी है। 90 डिग्री से अधिक)।

फोटो: iStock - tashechka