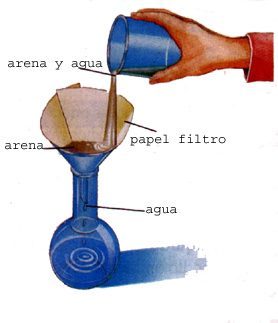
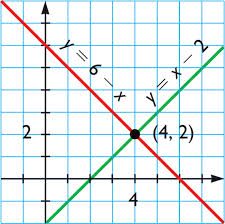
NS त्रिकोणमिति गणित की एक और शाखा है, जो प्रत्यक्ष या अप्रत्यक्ष रूप से इसमें और उस में हस्तक्षेप करता है विशेष रूप से त्रिभुजों के कोणों और भुजाओं के बीच संबंधों के अध्ययन से संबंधित है. मैं जानता हूँ इसका उपयोग अक्सर विशेष रूप से तब किया जाता है जब आपको सटीक माप प्राप्त करने की आवश्यकता होती है. उदाहरण के लिए, अन्य मुद्दों के बीच, भौगोलिक बिंदुओं और उपग्रह नेविगेशन सिस्टम के बीच की दूरी के मापन में, निकटतम सितारों के बीच की दूरी को मापने के लिए खगोल विज्ञान में त्रिभुज तकनीकों का उपयोग किया जाता है।
त्रिकोणमिति का उद्भव और अध्ययन प्राचीन शहर बेबीलोन से मिलता है, भारतीय, मुस्लिम और यूनानी गणितज्ञों के लिए विशेष अध्ययन रुचि का होना।
प्राचीन काल में त्रिकोणमितीय कार्यों को आम तौर पर अपने कोणों के संबंध में एक समकोण त्रिभुज के दो पक्षों के बीच के भागफल के रूप में परिभाषित किया जाता था, जबकि आज इन्हें अनंत श्रृंखला के रूप में या विभेदक समीकरणों के समाधान के रूप में वर्णित किया जाना आम बात है जो विस्तार को जटिल तक ले जाने की अनुमति देगा। संख्या और सकारात्मक और नकारात्मक दोनों मान।
छह बुनियादी त्रिकोणमितीय कार्य हैं: साइन, कोसाइन, टेंगेंट, कोटैंजेंट, सेकेंट और कोसेकेंट।.
यद्यपि अंतिम चार को पहले दो के संदर्भ में किसी भी चीज़ से अधिक परिभाषित किया जाएगा, उन्हें ज्यामितीय रूप से या उनके संबंधों के माध्यम से भी परिभाषित किया जा सकता है।
