त्रिकोणमितीय पहचान की अवधारणा एक अवधारणा है जिसका उपयोग गणित के क्षेत्र में चर त्रिकोणमितीय कार्यों को संदर्भित करने के लिए किया जाता है जो एक ज्यामितीय आकृति में पाया जा सकता है। त्रिकोणमिति गणित की वह शाखा है जो त्रिभुजों के विश्लेषण और अध्ययन में विशेषज्ञता रखती है, विशेष रूप से मौजूद विभिन्न कोणों के आकार, अर्थ और मूल्यों में। त्रिकोणमितीय पहचान तब उन मूल्यों का परिणाम होगी जो एक से दूसरे में परिवर्तनशील और बहुत विविध हैं।
गणित के कई तत्वों की तरह, अवधारणाएँ प्राचीन काल से मौजूद हैं जिनमें यूनानी दार्शनिकों ने पहले से ही ज्यामितीय आकृतियों के कोणों के कार्यों और मूल्यों की धारणाओं को स्थापित किया था। इन अवधारणाओं को केवल आधुनिकता में सुधार किया जाएगा, सत्रहवीं शताब्दी में जब उन्हें विभिन्न कोणों के बीच सभी प्रकार की गणना करने में सक्षम होने के लिए बीजगणितीय रूप से नोट किया गया था।
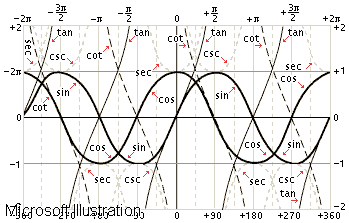
त्रिकोणमितीय सर्वसमिकाओं को मोटे तौर पर सभी संभावित कोण चर के रूप में परिभाषित किया जा सकता है जो एक ज्यामितीय आकृति में मौजूद हो सकते हैं। इन पहचानों को हमेशा ग्रीक अक्षरों जैसे अल्फा, बीटा, ओमेगा, आदि से दर्शाया जाता है। डिग्री सेंटीग्रेड जैसे तत्वों का उपयोग प्रत्येक पहचान के चरों को स्थापित करने के लिए भी किया जाता है। सबसे प्रसिद्ध वे हैं जो साइन और कोसाइन, साइन और स्पर्शरेखा आदि के बीच स्थापित होते हैं। त्रिकोणमितीय सर्वसमिकाएं सरलीकृत रूप हैं जो हमें त्रिकोणमिति के विभिन्न कार्यों को करने और जानने की अनुमति देती हैं। गणित के ये सभी प्रश्न, विशेष रूप से त्रिकोणमिति के, विभिन्न गणनाओं को व्यवस्थित करने का काम करते हैं जिन्हें प्रत्येक प्रकार के डेटा के विशिष्ट कार्यों से किया जाना चाहिए। त्रिकोणमितीय सर्वसमिकाएँ अत्यधिक परिवर्तनशील होती हैं और प्रत्येक त्रिकोणमितीय फलन (अर्थात मान) को प्रत्येक मामले के अनुसार विविध और विशिष्ट तरीकों से निरूपित करने के लिए अलग-अलग संभावनाएं प्रदान करती हैं।
